자료구조란 데이터를 효율적으로 이용할 수 있도록 저장하는 방법이며, 이를 통해 효율적인 알고리즘을 구현할 수 있다.
자료구조는 선형구조와 비선형구조로 구분된다.
4. 이진 트리(Binary Tree)
트리는 스택, 큐, 리스트와 달리 비선형 구조이다. 트리는 1개 이상의 노드를 가지는 유한 집합이다. 트리는 루트 노드를 가지며, 루트를 제외한 노드들은 분리되어 하나의 트리((서브트리)가 될 수 있다.
4.1 트리(Tree)
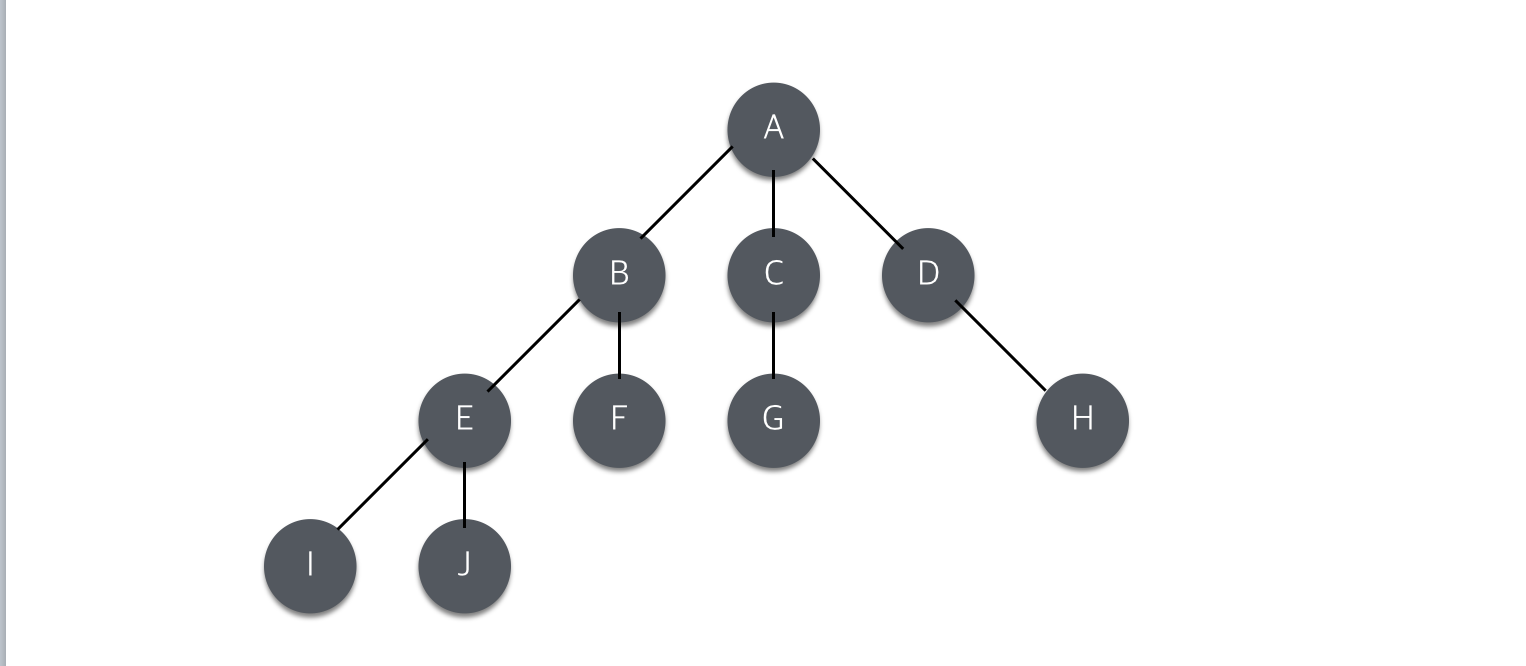
노드란, 위 그림에서 A, B, C, D … 의 값을 가지는 원과 원에서 뻗어져나오는 가지(Branch)를 포함한 것을 맗한다. 가장 상위에 있는 A를 루트 노드라고 하며, A와 같이 자식 노드(B, C, D)를 가지는 노드를 비단말 노드(Non-terminal node), 자식 노드를 가지지 않는 노드를(I, J, F, G, H) 단말 노드(Terminal node) 또는 리프(Leaf)라고 한다. 노드는 부모-자식 관계를 가지는데 A노드는 B, C, D 노드의 부모 노드이고, B, C, D 노드는 A노드의 자식 노드이다.
그리고 트리에서는 차수, 레벨, 높이(또는 깊이)라는 개념이 있는데, 차수는 트리 내의 어떤 노드가 가지는 자식 노드(=서브트리)의 수를 말한다. A의 차수는 3차이고, B는 2차, C는 1차이며 차수가 0일 경우 단말 노드가 된다.
레벨은 루트 노드를 1로 하고, 아래로 내려갈 떄마다 1씩 증가한다. 즉, 자식 노드는 부모 노드의 레벨에 1을 더한 값을 가진다. 높이(깊이)는 트리가 가지는 노드가 가지는 레벨 중 최대값을 말한다. 위의 그림에 나오는 트리는 높이가 4인 트리이다.
4.2 이진 트리(Binary Tree)
어떤 트리든 이진 트리로 표현이 가능하여, 구현이 단순한 편이라 가장 많이 쓰이는 트리이다. 이진 트리의 가장 큰 특징은 최대 차수가 2이다. 이진 트리에서는 왼쪽 서브트리와 오른쪽 서브트리를 구분하며 0개의 노드를 가질 수 있다.
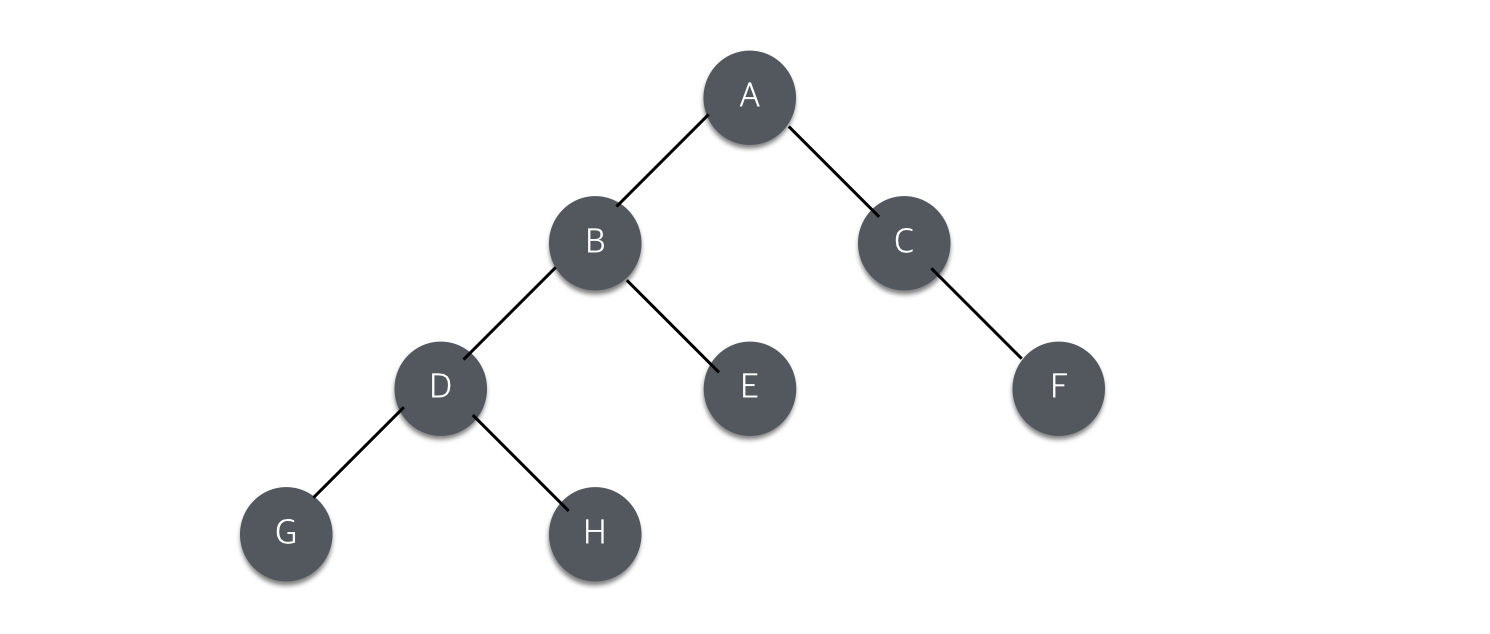
일반 트리와 이진 트리의 차이점은, 일반 트리에서는 0개의 노드를 가지는 트리가 없지만, 이진 트리에서는 공백 이진트리가 존재한다. 또한, 일반 트리에서는 자식 트리의 순서를 구분하지 않으나, 이진 트리에서는 자식의 순서를 구분한다는 2가지 차이점이 있다.
4.3 이진 트리의 ADT(Abstract Data Type)

4.4 Python Binary Tree 구현
class BinaryTree:
def __init__(self, data, left_child=None, right_child=None):
self.data = data
self.left_child = left_child
self.right_child = right_child
4.5 이진 트리 순회(Binary Tree Traversal)
트리에서 수행하는 몇 가지 연산 중 하나가 트리 순회이다. 트리 순회는 트리에 있는 모든 노드를 한 번씩만 방문하는 것을 말하는데, 한 노드에 방문했을 때 어떤 연산이 그 노드에서 수행하도록 구현한다. (예를 틀면, 출력)
순회에는 3가지 종류가 있는데 각각 중위(inorder) 순회, 전위(preorder) 순회, 후위(postorder) 순회가 있다. 순회는 구분하는 것은 각 서브트리의 루트 노드를 방문하는 순서와 연관이 있다. 전위 순회의 경우 루트 노드 - 왼쪽 서브트리 - 오른쪽 서브트리 순으로 순회가 이루어지며, 중위 순회는 왼쪽 서브트리 - 루트 노드 - 오른쪽 서브트리, 후위 순회는 전위 순회의 반대 방향으로 순회가 이루어진다.

중위 순회
class BinaryTree:
[....]
def inorder(self):
if self.left_child:
self.left_child.inorder()
print(self.data, end=" ")
if self.right_child:
self.right_child.inorder()위의 트리를 중위 순회한다면 결과는 4, 2, 5, 1, 3
전위 순회
class BinaryTree:
[....]
def preorder(self):
print(self.data, end=" ")
if self.left_child:
self.left_child.preorder()
if self.right_child:
self.right_child.preorder()위의 트리를 전위 순회한다면 결과는 1, 2, 4, 5, 3
후위 순회
class BinaryTree:
[....]
def postorder(self):
if self.left_child:
self.left_child.postorder()
if self.right_child:
self.right_child.postorder()
print(self.data, end=" ")위의 트리를 후위 순회한다면 결과는 4, 5, 2, 3, 1
레벨 순회
레벨 순회란 트리의 낮은 레벨부터 순차적으로 순회하는 방식이다. 레벨 1을 모두 순회한 이후 레벨 2, 레벨 2를 모두 순회한 이후 레벨 3을 순회하는 식이다.
레벨 순회는 큐를 활용하여 구현이 가능하다.
class BinaryTree:
[....]
def level_order(self):
queue = []
queue.append(self)
while queue:
node = queue.pop(0)
print(node.data)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)위의 트리를 레벨 순회한다면 결과는 1, 2, 3, 4, 5