자료구조란 데이터를 효율적으로 이용할 수 있도록 저장하는 방법이며, 이를 통해 효율적인 알고리즘을 구현할 수 있다.
자료구조는 선형구조와 비선형구조로 구분된다.
5. 이진 탐색 트리(Binary Search Tree)
이진 탐색 트리는 이진 트리로서 공백일 수 있고 공백이 아니라면 다음 4가지 성질을 만족해야한다.
- 모든 원소는 키를 가지며, 어떤 두 원소도 동일한 키를 갖지 않는다.(가지도록 확장할 수는 있음)
- 왼쪽 서브트리의 키 값들은 그 루트의 키값보다 항상 작다.
- 오른쪽 서브트리의 키 값들은 그 루트의 키값보다 항상 크다.
- 왼쪽과 오른쪽 서브트리도 모두 이진 탐색 트리이다.
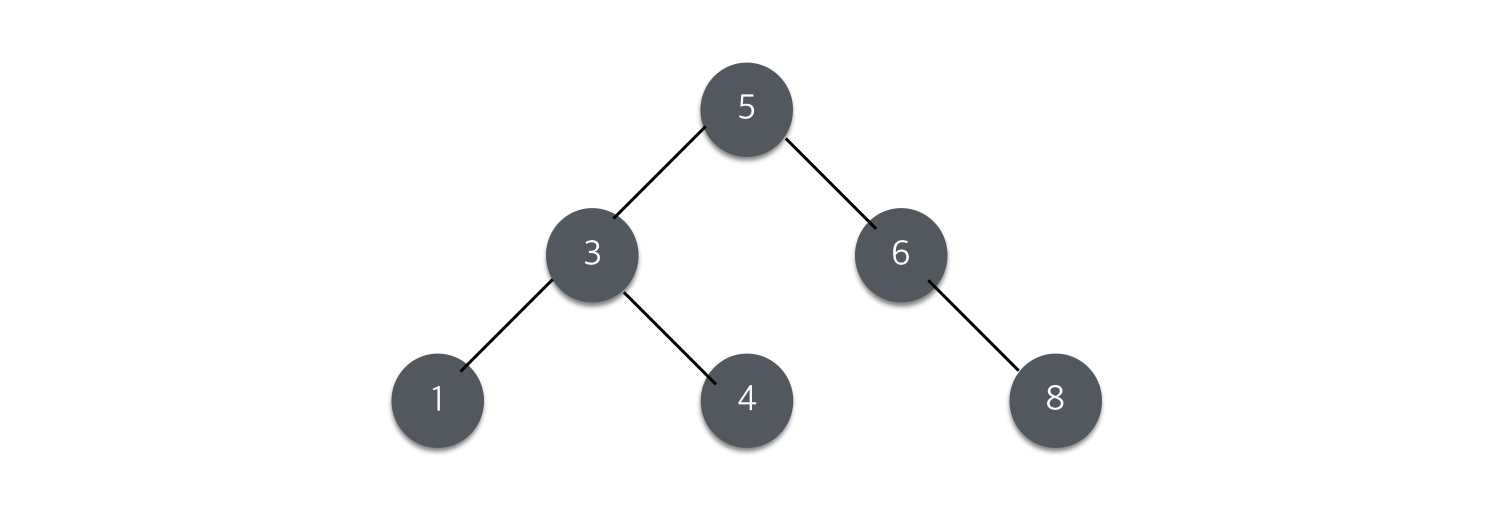
이진 탐색 트리는 위 그림처럼 왼쪽 서브트리는 그 루트(5)보다 모두 작고, 오른쪽 서브트리는 루트보다 모두 크다.
먼저, 트리에 사용될 노드를 구현하면
class BinaryTree:
class Node:
def __init__(self, key, data, leftNode=None, rightNode=None):
self.key = key
self.data = data
self.leftNode = leftNode
self.rightNode = rightNode
def isLeaf(self):
return not self.leftNode and not self.rightNode
def hasLeft(self):
return not (self.leftNode is None)
def hasRight(self):
return not (self.rightNode is None)노드에는 단말 노드인지 확인하는 메쏘드와 오른쪽, 왼쪽 자식이 있는지 확인하는 메쏘드를 포함했다.
5.1 BST 탐색
이진 탐색 트리는 이름에서 알 수 있듯이 이진 탐색을 하기에 매우 좋은 구조이다.
탐색의 방법은 가장 먼저, 찾으려는 값을 루트와 비교한 후 작으면 왼쪽 서브트리로 크면 오른쪽 서브트리로 진행하면 된다.
class BinarySearchTree:
def __init__(self, root=None):
self.root= root
self.size = 0
if root:
self.size = 1
def search(self, key):
temp = self.root
while temp:
if temp.key == key:
return self.root
if temp.key > key:
temp = temp.leftNode
else:
temp = temp.rightNode
return None
5.2 BST 삽입
삽입도 탐색과 유사하나 키가 중복되지 않게하려면 일단 트리 내에 중복된 키가 있는지부터 확인한다. 그 다음 키 값을 비교하여 해당 위치에 값을 삽입하면 된다.
class BinarySearchTree:
[....]
def insert(self, key, data):
if not self.search(key):
temp = self.root
while temp:
if temp.key > key:
if not temp.hasLeft():
temp.leftNode = Node(key, data)
self.size += 1
break
else:
temp = temp.leftNode
else:
if not temp.hasRight():
temp.rightNode = Node(key, data)
self.size += 1
break
else:
temp = temp.rightNode
5.3 BST 삭제
동일하게 삭제도 해당 키값을 찾은 후 삭제해주면 된다.
class BinarySearchTree:
[....]
def delete(self, key):
if self.size > 1:
temp = self.root
while temp:
if temp.leftNode and temp.leftNode.key == key:
temp.leftNode = None
self.size -= 1
break
if temp.rightNode and temp.rightNode.key == key:
temp.rightNode = None
self.size -= 1
break
if temp.key > key:
temp = temp.leftNode
else:
temp = temp.rightNode