자료구조란 데이터를 효율적으로 이용할 수 있도록 저장하는 방법이며, 이를 통해 효율적인 알고리즘을 구현할 수 있다.
자료구조는 선형구조와 비선형구조로 구분된다.
8. AVL(Adelson-Velskii and Landis) 트리
이진 검색 트리에서 최악의 경우 시간 복잡도는 O(n)인데 편향 이진 트리일 경우 발생한다. 그래서 높이에 제한을 두어 최악의 경우 복잡도를 O(log n)으로 만들기위해 개발된 자료구조가 균형 이진 검섹 트리이다.
균현 이진 검색 트리는 루트를 중심으로 왼쪽 트리와 오른쪽 트리의 높이 차가 일정한 트리를 말한다. (부분 트리도 모두 양쪽의 높이 차가 일정해야한다) 만약 높이 차가 0이라면 완전 균형 이진 검색 트리라고 하며, 차이가 1일 때 AVL 트리이다.
즉, AVL 트리는
- 이진 검색 트리
- 어떤 노드의 오른쪽 자식 트리와 왼쪽 자식 트리의 높이 차이가 1 이하인 트리
2 가지 속성을 만족한다.
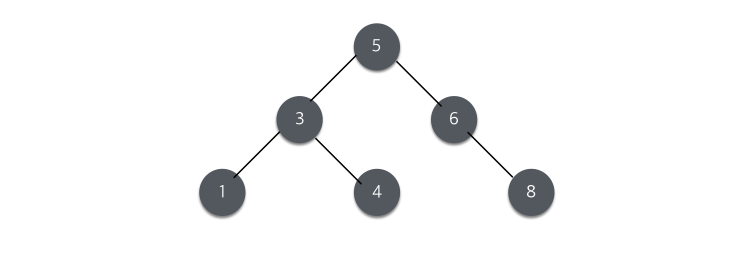
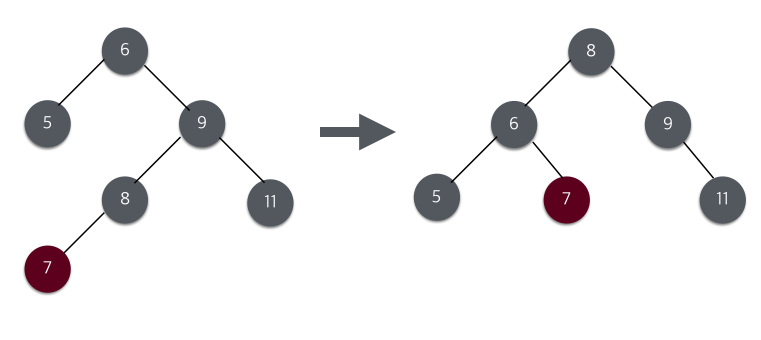
위 그림의 트리는 이진 검색트리이며, 1, 3, 4, 5, 6, 8 모든 노드에서 왼쪽 자식 트리와 오른쪽 자식 트리의 높이 차가 1이하이므로 AVL 트리이다.
트리의 회전
균형 이진 검색 트리에서는 삽입, 삭제 등이 일어나 트리 구조가 변하였을 때 트리의 속성을 유지하기위해서 트리를 회전시킨다. 트리에 노드가 삽입 또는 삭제되면 특정 노드의 자식 트리 높이가 1 증가하거나 1 감소함을 말한다. 한쪽 자식 트리의 높이가 증가하므로 높이 차가 일관성을 잃을 수 있다. 그렇기때문에 노드의 이동을 통해 트리의 속성을 유지하여야하는데 높이 차와 이진 검색 트리라는 특성을 모두 유지하기위해 노드를 이동시키다 보면 노드들이 일정한 방향으로 회전함을 알 수 있다.
회전의 종류는 단순 회전과 이중 회전(두번의 단순 회전)이 있다.
트리에 새로운 노드를 삽입 시 회전이 필요한 경우는 4가지이다.
- 노드 A의 왼쪽 자식의 왼쪽 트리에 노드가 삽입되는 경우
- 노드 A의 오른쪽 자식의 오른쪽 트리에 노드가 삽입되는 경우
- 노드 A의 왼쪽 자식의 오른쪽 트리에 노드가 삽입되는 경우
- 노드 A의 오른쪽 자식의 왼쪽 트리에 노드가 삽입되는 경우
첫 번째, 두 번째의 경우는 단순 회전만으로 해결이 가능하지만, 세 번째, 네 번째의 경우 이중 회전이 필요하다.
단순 회전
왼쪽 왼쪽 회전(LL회전)
첫 번째 경우 필요한 회전이다.
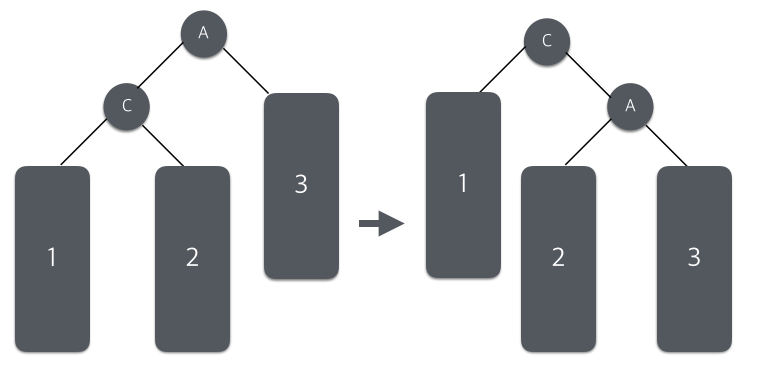
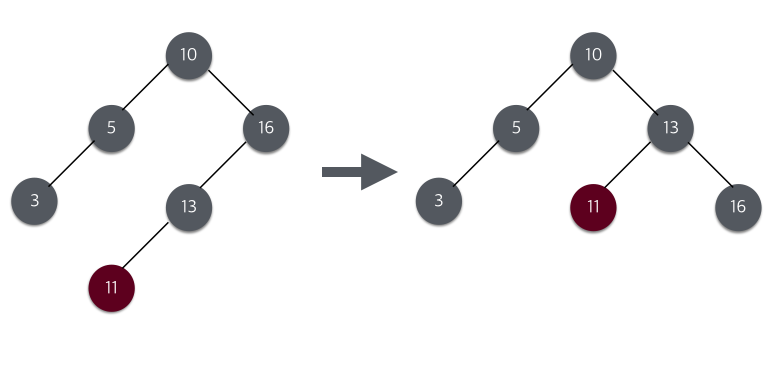
11이 삽입되어 균형이 깨어졌으므로 16을 중심으로 LL회전하여 균형을 맞춘다. 16이 한칸, 13이 한칸, 11이 한칸 이동하면 위의 그림과 같은 결과가 나온다.
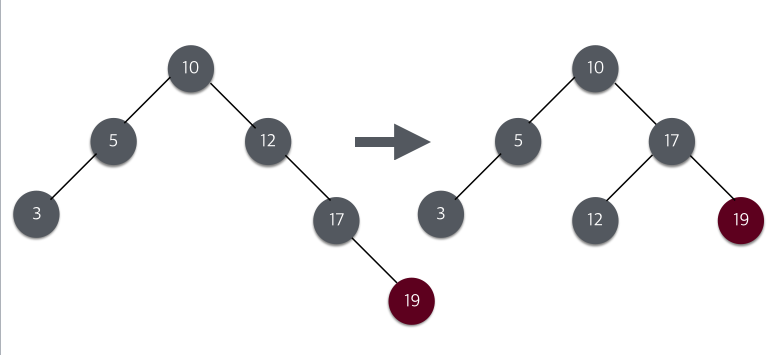
오른쪽 오른쪽 회전(RR회전)
두 번째 경우 필요한 회전이다. LL회전과 반대
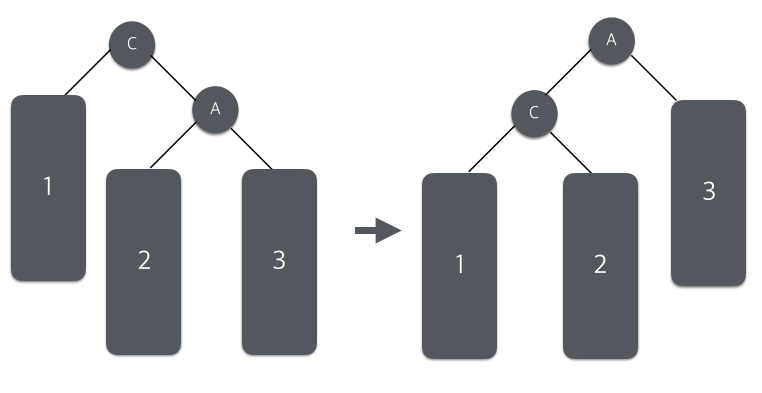
이중 회전
왼쪽 오른쪽 회전(LR회전)
세 번째 필요한 회전으로 단순 회전 한번만으로 해결이 어렵기때문에 두번의 회전을 통해 해결한다. LR회전은 이름처럼 L회전과 R회전을 순서대로 수행한다.
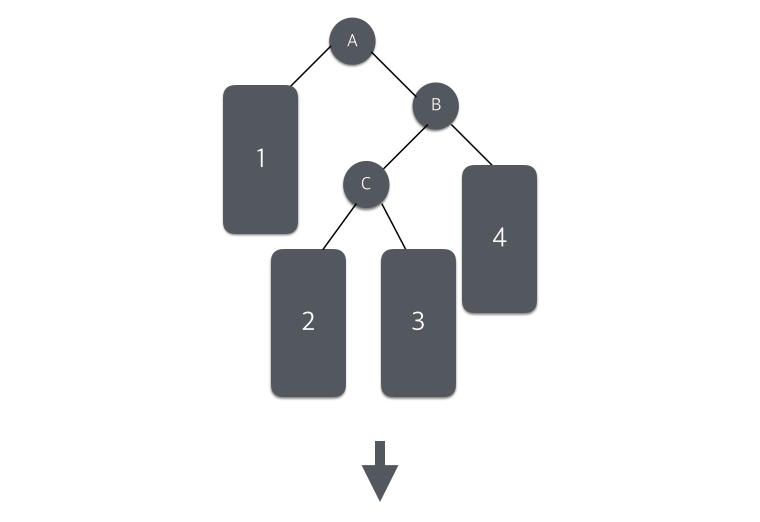
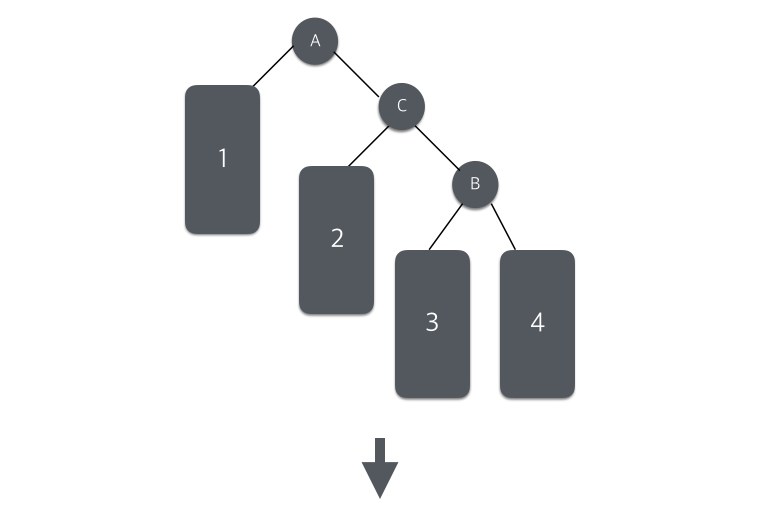
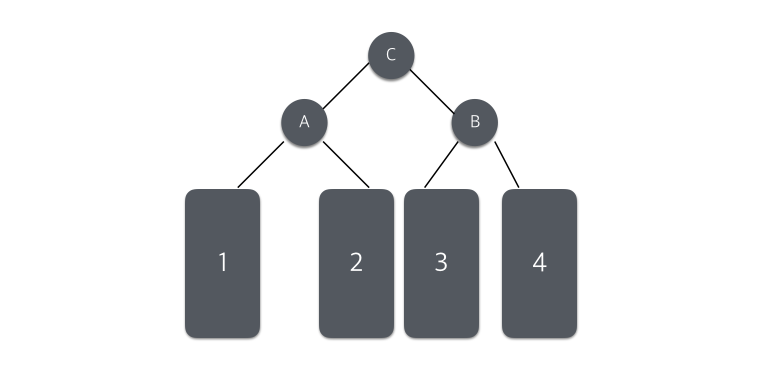
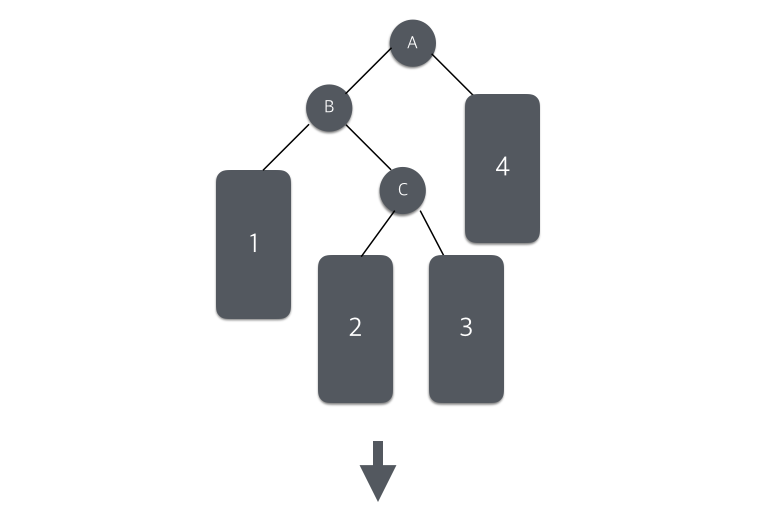
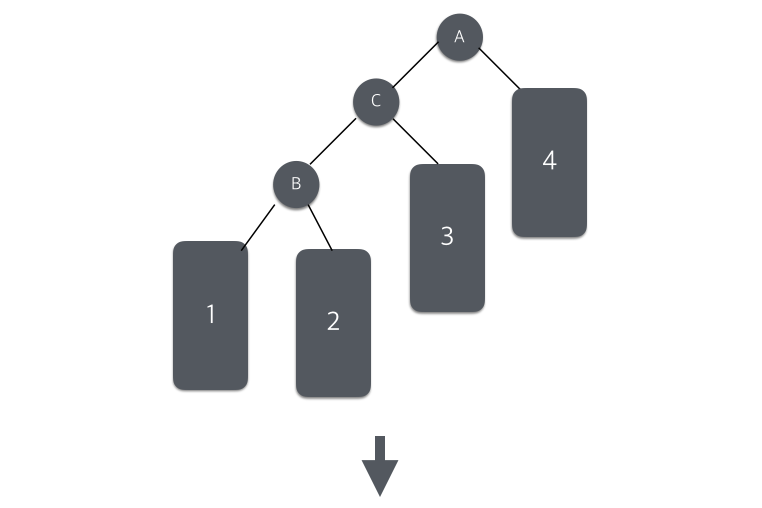
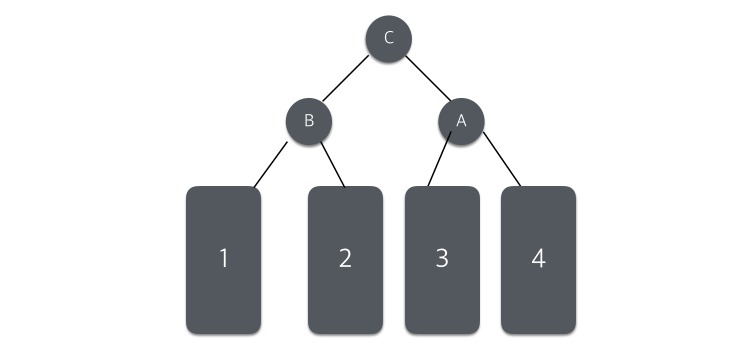
B를 중심으로 왼쪽 회전을 실행 후, A에서 오른쪽 회전을 실행하여 트리의 균형을 맞춘는 방법이다.
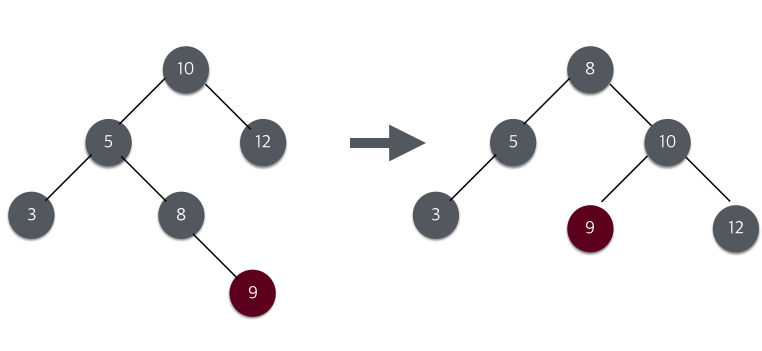
9가 삽입되어 균형이 깨어진 상태에서 균형을 다시 맞추기위해 5를 중심으로 왼쪽 회전 한번, 10을 중심으로 오른쪽 회전을 실행하여 다시 균형을 맞추었다.
오른쪽 왼쪽 회전(RL회전)
네 번째 경우는 LR회전에서 L회전, R회전의 순서만 바뀐다.