Dynamic Programming(DP, 동적계획법)
큰 문제를 작은 문제로 나눠서 푸는 알고리즘으로 분할 정복법(Divide and Conquer)과 유사하다. 해결된 문제의 답을 저장해두고 그것을 재활용하여 해결된 문제를 다시 푸는 비효율을 제거한다. 공간복잡도를 늘리고 시간복잡도를 줄이는 방식이다.
DP는 다음 2가지 특성을 만족해야만 사용할 수 있다.
- Overlapping subproblem
- Optimal substructure
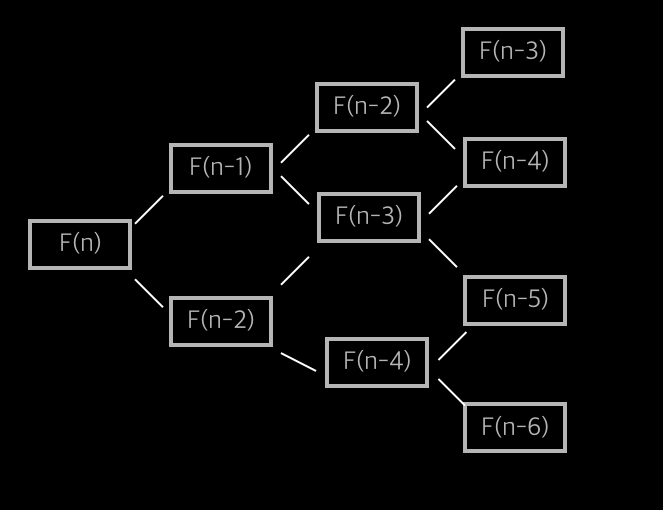
피보나치 수열은 DP로 풀 수 있는 문제의 대표적인 예이다. 먼저 Overlapping subproblem은 겹치는 부분 문제를 이야기하는데 즉, F(n-2), F(n-3), F(n-4) 등과 같이 같은 값을 여러번 구하는 것을 말한다. Optimal substructure은 나눠진 작은 문제의 해답으로 원래 문제의 정답을 찾을 수 있는 특징을 말한다. F(n)의 답은 나눠진 작은 문제인 F(n-1)과 F(n-2)로 구할 수 있다.
예제
예제는 BOJ에서 직접 풀어본 문제들이다.
1463번
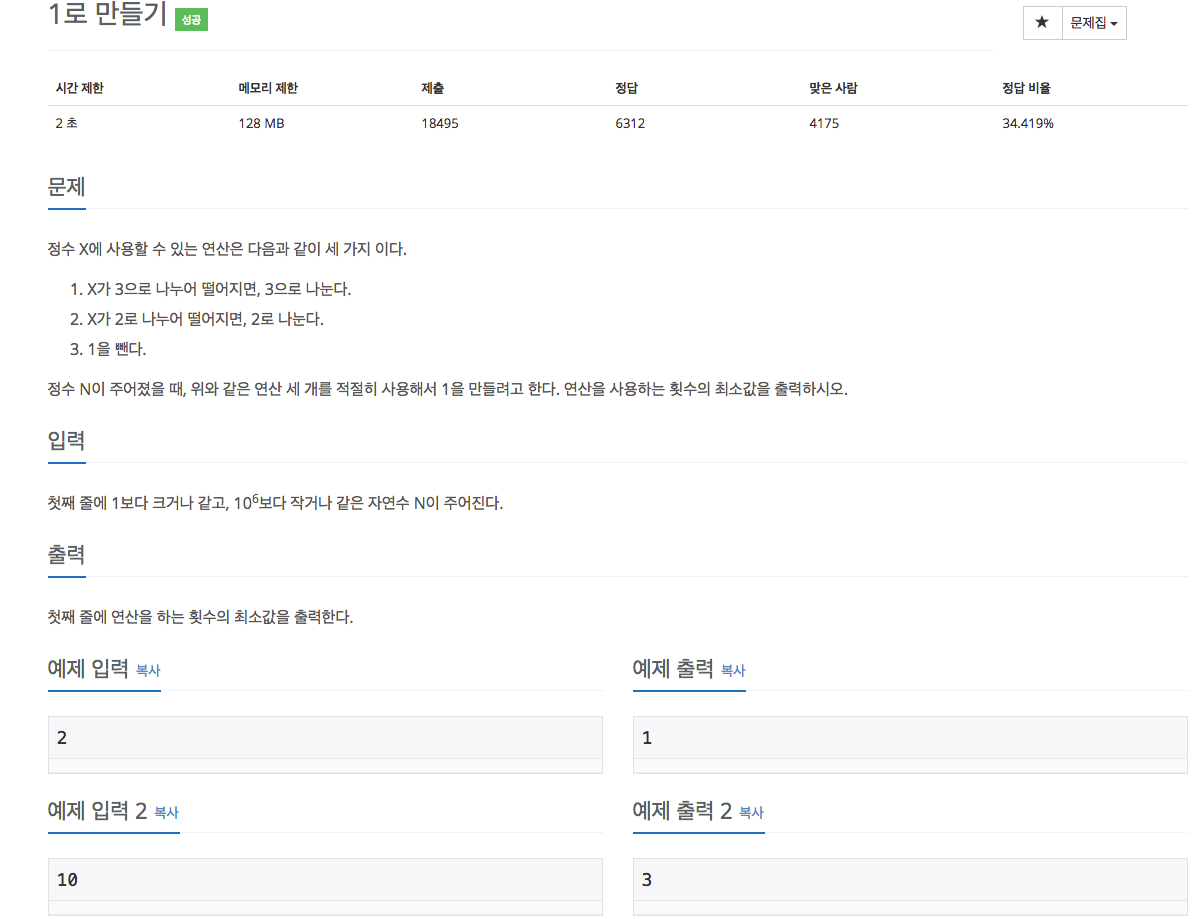
간단하게 생각하면 X가 2로 나누어지면 2로 나누고, 3으로 나누어질 때는 3으로 나누는 방식으로 풀 수 있을 것 같지만 예외가 존재한다. 예를 들어 10은 2로 나눌 경우 4번(10->5->4->2->1)의 연산이 필요하지만 최소값은 3번(10->9->3->1)이다.
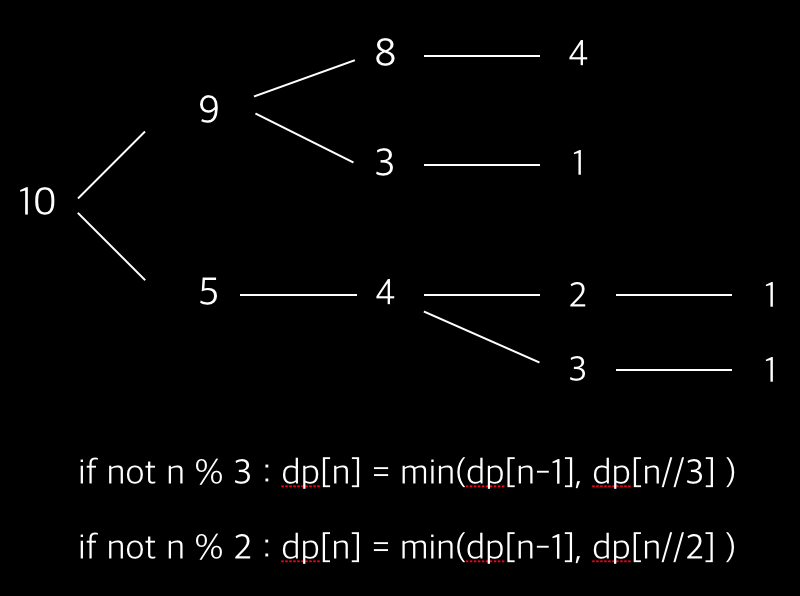
10의 경우 9(X-1), 5(x/5) 중 최소 연산으로 1이 되는 것을 선택하면 된다. 9는 8, 3 중 1로 만드는데 필요한 최소 연산 수를 각각 구하여 더 적은 연산이 필요한 연산(나누기 3, 뺴기 1) 을 선택하면 된다.
즉 10은 9, 5라는 작은 문제로 나누어지고 작은 문제의 정답을 이용하여 본래 문제의 정답을 찾을 수 있다. 또한 9->(8 or 3), 5->4->(2 or 3)에서 3과 같이 겹치는 부분이 등장한다.
이 문제의 python 코드는 아래와 같다.
x = int(input())
dp = [0 for _ in range(x+1)]
dp[1] = 0
for i in range(2, x+1):
dp[i] = dp[i-1] + 1
if not i % 2 and dp[i] > dp[i//2] + 1:
dp[i] = dp[i//2] + 1
if not i % 3 and dp[i] > dp[i//3] + 1:
dp[i] = dp[i//3] + 1
print(dp[x])
11726번
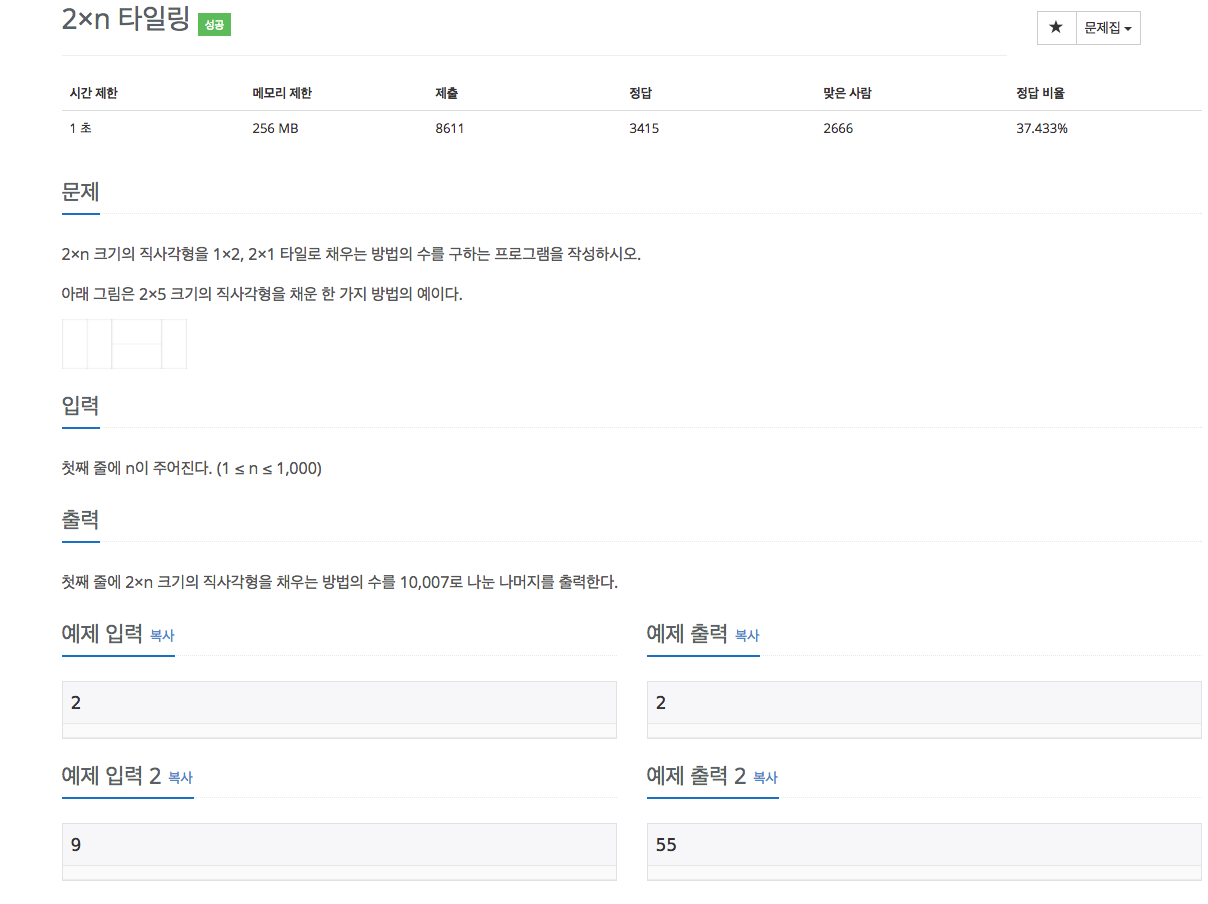
2x1, 1x2 타일이 마지막에 올 수 있는 경우는 아래의 2가지 밖에 없다.

즉, 1x2가 왔을 경우와 2x1가 2개 왔을 때 뿐이다. 그러므로 두 경우를 합하면 길이가 n인 2xn 크기의 직사각형을 채우는 방법은 1x2가 마지막에 오는 경우와 2x1이 마지막에 오는 경우를 더 하면 된다.
이 문제의 python 코드는 아래와 같다.
n = int(input())
dp = [0 for _ in range(n+1)]
dp[1] = 1
dp[0] = 1
for i in range(2, n+1):
dp[i] = dp[i-1] + dp[i-2]
print(dp[n]%10007)
10844번
인접한 수가 1차이나는 수이므로 ####3의 경우 앞에 올 수 있는 숫자는 ###2 또는 ###4뿐이다. 첫번째 자리를 제외하고(0이 올 수 없으므로) 0~9까지 각각의 수에 올 수 있는 경우가 조금씩 다르다. 따라서 n자리 수일 때 1이 오는 수는 dp[n][1]로 표현이 가능하며 n=1일 때를 제외하고는 n마다 10개의 값을 가진다.
즉, dp[n][m] = dp[n-1][m-1] + dp[n-1][m+1]로 표현된다.(0 < m < 9)
(m=9, dp[n][m] = dp[n-1][m-1])
(m=0, dp[n][m] = dp[n-1][m+1])
이 문제의 python 코드는 아래와 같다.
n = int(input())
result = [[0 for _ in range(10)] for _ in range(n+1)]
for i in range(1, 10):
result[1][i] = 1
for i in range(2, n+1):
for j in range(10):
if j-1 >= 0:
result[i][j] += result[i-1][j-1]
if j+1 <= 9:
result[i][j] += result[i-1][j+1]
ans = 0
for i in range(10):
ans += result[n][i]
print(ans%1000000000)
11057번
오르막 수도 내리막 수와 비슷하게 접근하면 된다. ####3 이전에 올 수 있는 수가 ###0~3까지 이므로
dp[n][m] = sum(dp[n-1][m] + dp[n-1][m-1]+ dp[n-1][m-2]….)
줄여보면 dp[n][m] = dp[n][m-1] + dp[n-1][m]임을 알 수 있다.
따라서 이 문제의 python 코드는 아래와 같다.
n = int(input())
dp = [[0 for _ in range(10)] for _ in range(n+1)]
for i in range(10):
dp[1][i] = 1
for i in range(2, n+1):
for j in range(10):
dp[i][j] = dp[i][j-1] + dp[i-1][j]
ans = 0
for i in range(10):
ans += dp[n][i]
print(ans % 10007)